今回は3.一次関数と二次関数のグラフを解説します。
女子美術大学附属高校2010年度数学入試問題3.関数のグラフ 問題
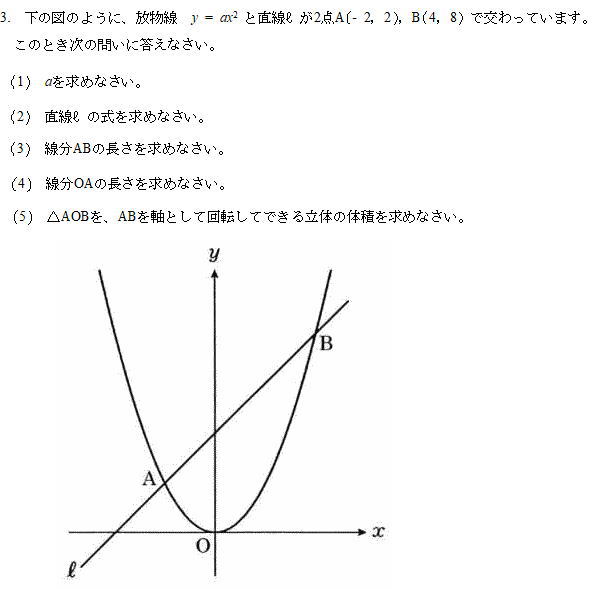
(1) aを求めなさい。
(2)直線ℓの式を求めなさい。
(3)線分ABの長さを求めなさい。
(4)線分OAの長さを求めなさい。
(5) △AOBを、ABを軸として回転してできる立体の体積を求めなさい。
女子美術大学附属高校2010年度数学入試問題3.関数のグラフ (1) 解説解答
解説解答

女子美術大学附属高校2009年度数学入試問題3.関数のグラフ (2) 解説解答
(2)直線ℓの式を求めなさい。
解説解答
直線ℓは 2点 A( – 2,2),B(4,8)を通る直線なので 傾きは
切片は 8 – 4 = 4
答 y = x + 4
女子美術大学附属高校2009年度数学入試問題3.関数のグラフ (3) 解説解答
(3)線分ABの長さを求めなさい。
解説解答
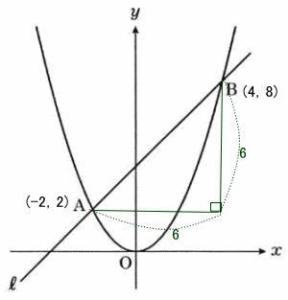
点Aからx軸に平行は直線を引き、点Bからy軸に平行な直線を引く。その交点をCとする。
点Cの座標は(4,2)
AC=4-(-2)=6,BC=8-2=6,∠C=90°
よって ⊿ABCは直角二等辺三角形となる。
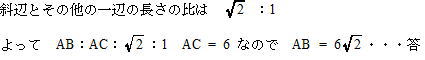
女子美術大学附属高校2009年度数学入試問題3.関数のグラフ (4) 解説解答
(4)線分OAの長さを求めなさい。
解説解答
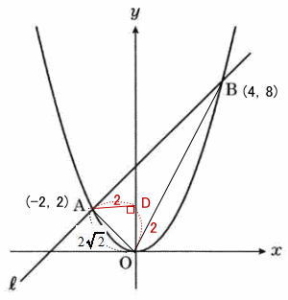
(3)と同様に 点Aからx軸に平行な直線を引きy軸との交点をDとする。
⊿OADは AD=2, OD=2, ∠ADO=90°の二等辺三角形
よって線分OAは⊿OADの斜辺なので
女子美術大学附属高校2009年度数学入試問題3.関数のグラフ (5) 解説解答
(5)△AOBを、ABを軸として回転してできる立体の体積を求めなさい。
解説解答
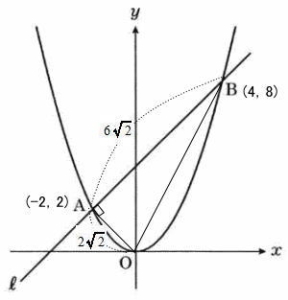
(3)より∠BAC=45° ,(4)より∠DAO=45°, よって ∠OAB=90°
⊿AOBをABを軸として回転して出来る立体は AOを半径, ABを高さとする円錐となる。
