晃華学園中学校受験算数過去問研究
今回は(2)(3)の平面図形の問題を解説します。(2)の①は平面図形の求角の問題としては塾で繰り返し学習する内容ですが、②の求積は初めてでとまどった受験生も多かったでしょう。①がヒントになっています。晃華学園中学校頻出の平面図形問題は、類題を多くこなし”ヒラメキアタマ”になりましょう。
算数入試問題 平面図形にチャレンジ
晁華学園中学校2015年度算数入試問題(2)平面図形 問題
晁華学園中学校2015年度算数入試問題(2)平面図形①解説解答
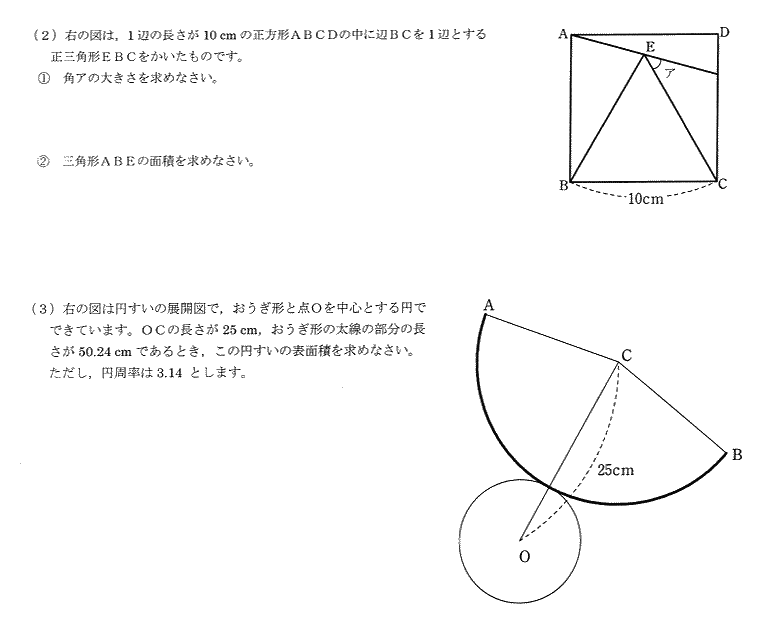
| (2) ① 角アの大きさを求めなさい。 |
| 解説 |
 |
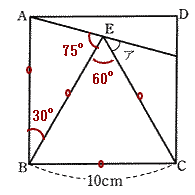| 三角形ABEは、AB = EBなので二等辺三角形。角ABEは90°- 60°= 30°なので 角EAB = 角AEB = (180 – 30)÷2 = 75° 角BECは正三角形の内角の1つなので60° よって 角ア = 180° – ( 75° + 60°) = 45° |
| 答 45° |
| (2) ① ABEの面積を求めなさい。 |
| 解説 |
 |
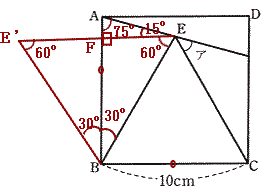| 点Eから辺ABに垂直になるように直線を引き、その交点をFとする。図のように三角形EFBと合同な三角形を直線FBの反対側に描くと、三角形EE’B正三角形になる。 三角形ABEの高さEFは１辺10cmの正三角形の半分の長さなので、5cm。 よって 三角形ABEの面積は 10×5÷2 = 25(c㎡) |
| 答 25c㎡ |
晁華学園中学校2015年度算数入試問題(2)平面図形②解説解答
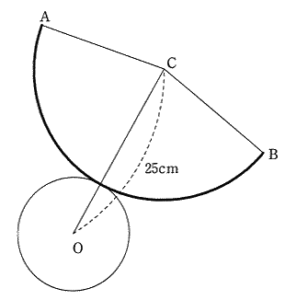
| (3) 右の図は円すいの展開図で、おうぎ形と点Ｏを中心とする円でできています。 OCの長さが25cm, おうぎ形の太線の部分の長さが50.24cmであるとき、 この円すいの表面積を求めなさい。 |
 |
| 解説 |
 したがって おうぎ形の半径(=円すいの母線)は 25 – 8 = 17cm 円すいの表面積は  |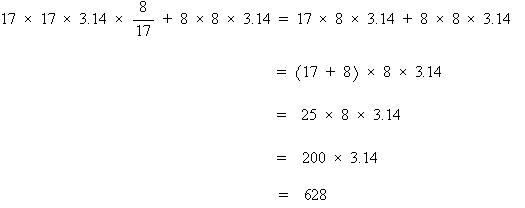
| 答 628c㎡ |