城北高等学校過去問研究
2020年度城北高等学校数学入試問題は昨年同様大問5題構成でした。[1]小問集合4問,[2]図形に関する小問集合3問 [3]方程式の応用 [4]関数のグラフ [5]空間図形題が出題されました。
今回は2..平面図形に関する問題3問を解説します。角の二等分線の定理,中点連結定理,円に内接する四角形の性質を理解して解きましょう。
記事の作成者:プロ家庭教師集団スペースONEとは
城北高校2020年度数学入試問題2.平面図形
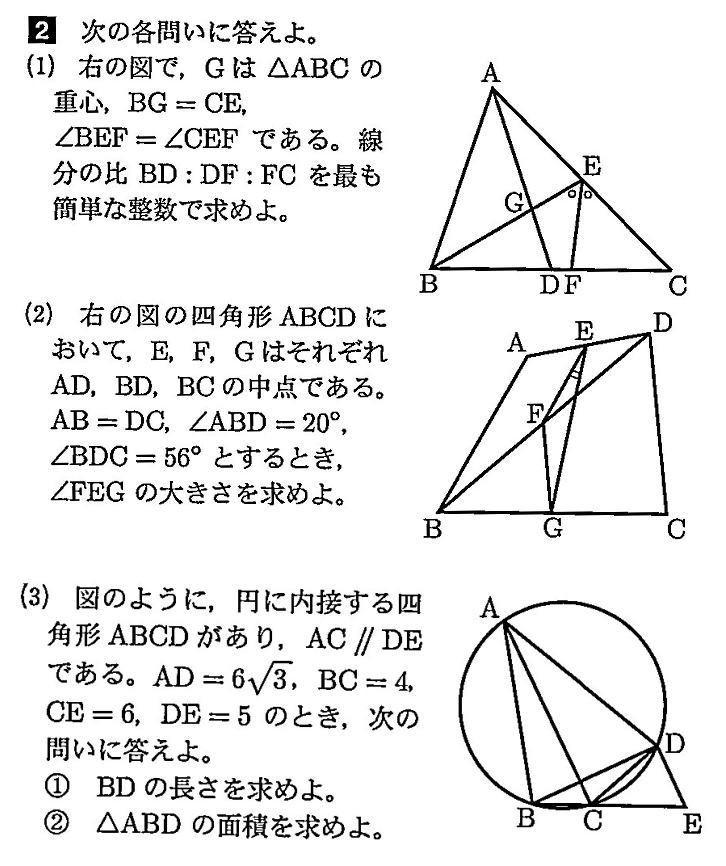
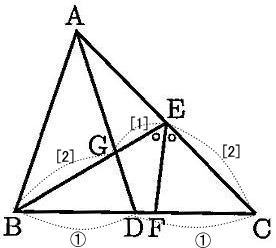
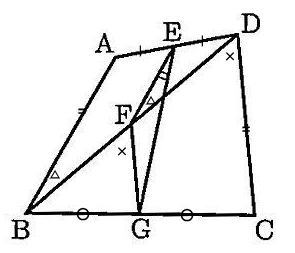

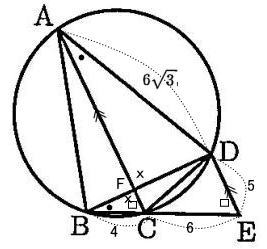
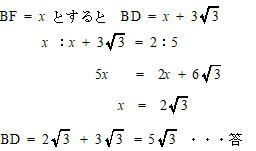
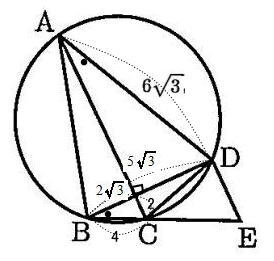
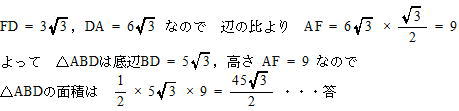
オンライン家庭教師も在籍中!「お問い合わせ種別」の欄を選択ください。
営業時間:AM 10:00 〜PM 9:00