東京都立高等学校共通数学過去問研究
2020年度をもってグループ作成問題は廃止されますが、 進学指導特別推進校(日比谷高校・西高校・国立高校・八王子東高校・戸山高校・青山高校・立川高校)と進学指導特別推進校(新宿高校・進学重視型単位制高校の国分寺高校)、進学指導推進校(進学重視型単位制高校の墨田川高校)が国語・数学・英語3科目とも自校作成問題となります。
よって 2020年度までグループ作成問題を利用していた都立大泉高校,都立白鷗高校,都立領国高校は共通問題が出題されます。
都立高校受験生は過去問を通して合格対策をとりましょう。
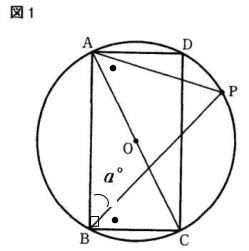
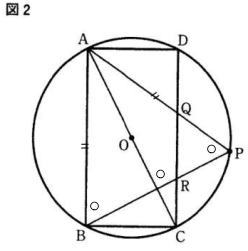
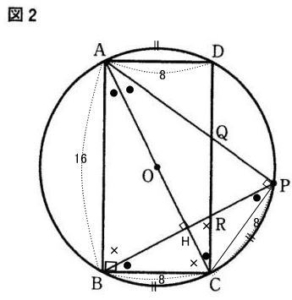
2021年度都立高校数学入試問題は、例年通りの出題構成で、内容は1.小問集合9問(含作図) 2.文章題(規則と平面図形) 3.一次関数のグラフ 4.平面図形 5.立体図形でした。
今回は 4.平面図形を解説します。