東海大学附属浦安高校2020年度数学入試問題は例年通り大問5大構成で、1,2,小問集合,3.関数,4.平面図形(円の性質), 5.空間図形が出題されました。標準レベルの出題です。教科書の巻末問題を中心に学習をしましょう。
今回は5.空間図形(正四角錘)を解説します。
東海大学附属浦安高校2020年度 数学入試問題 5. 空間図形 問題
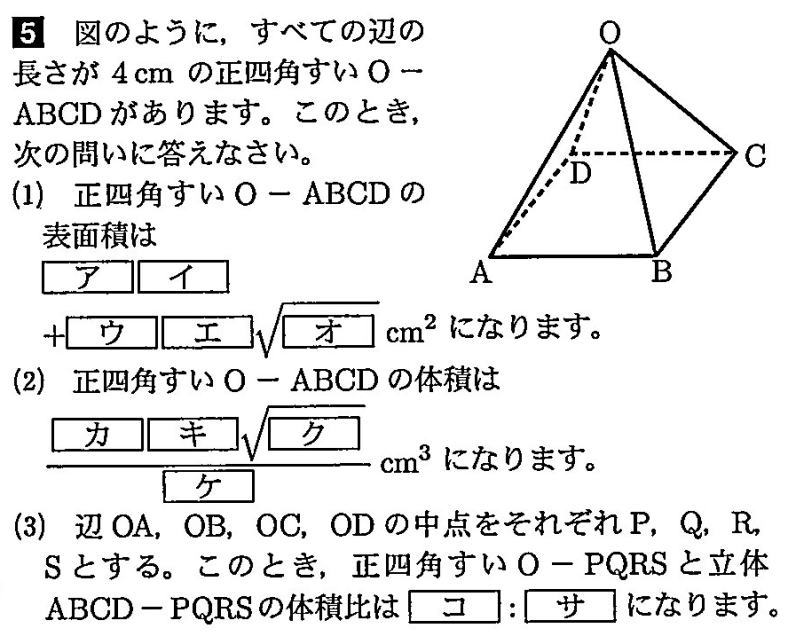
東海大学附属浦安高校2020年度 数学入試問題 5. 空間図形 (1)解説解答
(1) 正四角すいO-ABCDの表面積
解説解答
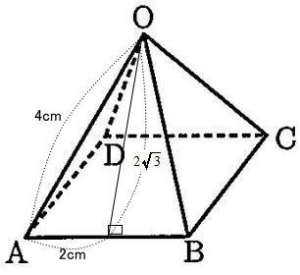
正三角形OABの底辺をAB(4cm)とすると、高さは
正四角すO-ABCDの表面積 = 1辺4cmの正三角形の面積×4 + 1辺4cmの正方形の面積
答 ア 1,イ 6,ウ 1,エ 6,オ 3
東海大学附属浦安高校2020年度 数学入試問題 5. 空間図形 (2)解説解答
(2) 正四角すいO-ABCDの体積
解説解答
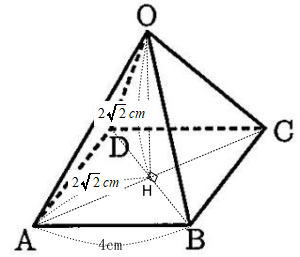
頂点Oから底面ABCDに垂線を下ろし、その交点をHとする。
Hは底面正方形ABCDの対角線の交点となり、対角線の中点となる。
正四角すいO-ABCDの体積は
答 カ 3,キ 2,ク 2,ケ 3
東海大学附属浦安高校2020年度 数学入試問題 5. 空間図形 (3)解説解答
(3) 辺OA,OB,OC,ODの中点をそれぞれP,Q,R,Sとする。このとき正四角すい-PQRSと立体ABCD-PQRSの体積比は[コ]:[サ]になります。
解説解答
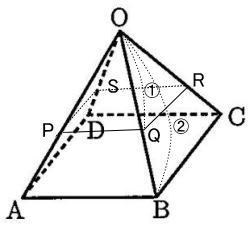
OH:OP = OB:OQ = OC:OR = OD:OS=2:1
よって 正四角すいO-ABCDと四角すO-PQRSの体積比は
立体ABCD-PQRSの体積 = 正四角すいO-ABCDの体積 – 四角すいO-PQRSの体積
よって 正四角すい-PQRSと立体ABCD-PQRSの体積比は
1:8 – 1 = 1:7
答 コ 1,サ 7
