桜蔭学園 桜蔭中学校高等学校算数過去問対策研究
2009年度は 計算３問,場合の数,数の性質,平面図形の求積,立体図形の展開図,平面状の点の移動の大問５題構成でした。
昨年度より問題数は１題少なくなりましたが、難易度と要求される処理能力は昨年が平易な問題で構成されていたためか、難易度を上げてきています。
算数入試問題（求積にチャレンジ）
等積移動がポイントになります。桜蔭中学校の受験生にとっては何度も練習した学習内容でしょう。
桜蔭中学校2009年度算数入試問題 Ⅱ平面図形 問題
桜蔭中学校中学校2009年度算数入試問題Ⅱ平面図形 (1)解説解答
（１） アとイの斜線の部分の面積の和を求めなさい。
解説
下図の通り アの面積 = ウの面積。
よって 中心角９０°の扇形と直角三角形の和になる。
３×３×３.１４÷４＋３×３÷２＝11.565
答 11.565ｃ㎡
桜蔭中学校2009年度算数入試問題Ⅱ平面図形 (2)解説解答
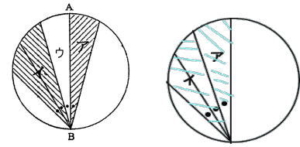
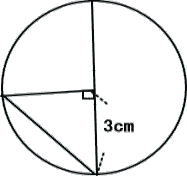
（２） イの斜線の部分の面積を求めなさい。
解説
アとイの斜線の部分の面積の和（11.565ｃ㎡）からアの面積を引く。
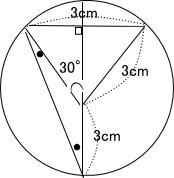
アの面積は 中心角30°の扇形と底辺3cm 高さ1.5cmの三角形の和なので、
３×３×3.14÷12 + 3×1.5÷2 = 4.605
イ の面積 11.565 – 4.605 = 6.96
答 6.96ｃ㎡