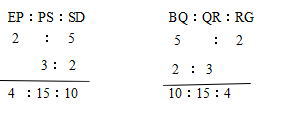東京都立戸山高等学校数学過去問研究
戸山高校の一般入試では7:3の比率に換算された学力検査の換算点と調査書の換算点の合計点による総合成績の上位者から順に合格候補者を決定します。
2012年度東京都立戸山高校自校作成数学入試問題は 例年通りの問題構成で 1.小問集合 2.~4 大問(枝問各3)でした。
出題内容は 1.小問5問(含作図問題) 2.一次関数と二次関数のグラフ 3.平面図形(平行四辺形)の証明と分割 4.立体図形上の点移動と転回図形 でした。
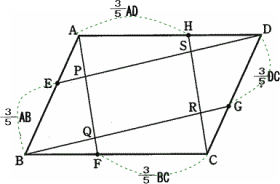
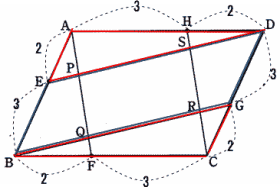
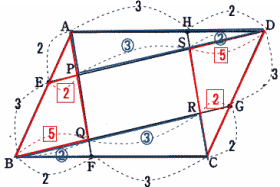
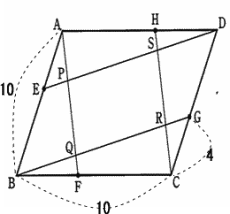
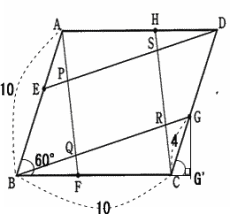
今回は 3.平面図形(平行四辺形)の証明と分割を解説します。
東京都立戸山高校2012年度 数学入試問題 3. 平面図形 問題