2007年度芝中学・高等学校過去問研究
平面図形の問題のなかでも相似形の求積・辺の長さは芝中学校では毎年の定番問題です。芝中学を志望する生徒は、自分で相似形の図形をを見つけるこのような問題は類似問題を十分に練習して確実に解けるようにしましょう。
芝中学校2007年度 算数入試問題 平面図形(相似比と面積比) 問題
記事の作成者:プロ家庭教師集団スペースONEとは
芝中学校2007年度算数入試問題 平面図形(相似比と面積比)
平面図形の問題のなかでも相似形の求積・辺の長さは芝中学校では毎年の定番問題です。芝中学を志望する生徒は、自分で相似形の図形をを見つけるこのような問題は類似問題を十分に練習して確実に解けるようにしましょう。
芝中学校2007年度 算数入試問題 平面図形(相似比と面積比) 問題
下図において、四角形DEFG、四角形GHCはともに正方形で、角AJD=90°、GH=2cm,FH=5cmとします。 |
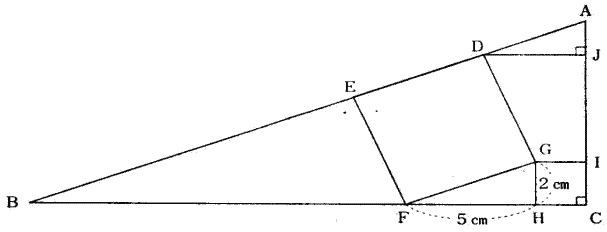 |
(1) AJの長さは( )cmです。 |
| (2) 三角形ABの面積は( )c㎡です。 |
| AJの長さは( )cmです。 |
| 解説 |
| 下図において、点Gから辺DJ上に垂線を引き交点をKにすると、三角形FHGと合同な三角形DKGができます。 |
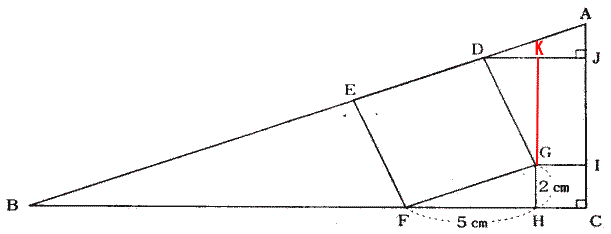 |
| このときJK=2cm DK=2cmです。 |
| また 三角形FHGと三角形DJAは相似な三角形です。 |
| 相似比は 5:2なので 辺DJ:辺AJ=5:2=4:X 辺AJ=1.6cm |
| 答 1.6cm |
| 三角形ABCの面積は( )c㎡です。 | |
| 解説 | |
| 下図において、辺AC=1.6+5+2=8.6cm | |
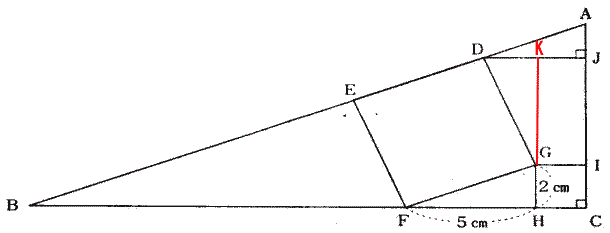 | |
| 三角形ABCと三角形GFHも辺の比が5:2の相似な三角形です。 | |
| 辺AC(高さ)=8.6cm | |
| 辺BC(底辺)=8.6÷2×5=21.5cm | |
| 三角形ABCの面積は 21.5×8.6÷2=92.45 | |
|
オンライン家庭教師も在籍中!「お問い合わせ種別」の欄を選択ください。
営業時間:AM 10:00 〜PM 9:00