秋田県立高等学校数学過去問研究
今回は 秋田県立高校数学入試問題5の平面図形問題を解説します。
5はⅠ,Ⅱ,Ⅲの中から指示された問題を答えます。それぞれ段階的に難易度が高くなっています。
Ⅲは補助線を引いたり、相似形を見つけることが正答への道です。
5はⅠ,Ⅱ,Ⅲの中から指示された問題を答えます。それぞれ段階的に難易度が高くなっています。
Ⅲは補助線を引いたり、相似形を見つけることが正答への道です。
記事の作成者:プロ家庭教師集団スペースONEとは
秋田県立高校2010年度 数学入試問題 5-Ⅲ 平面図形
| Ⅲ 正方形ABCD について,次の(1)~(3)の問いに答えなさい。 |
| (1) 図1のように,辺AD,BC の中点をそれぞれ点M,N とする。 折り目が点C を通り,点D が線分MN上にくるように折り返す。 点D が移った点をE とし,折り目を線分FC とする。 ∠ EFC の大きさを求めなさい。 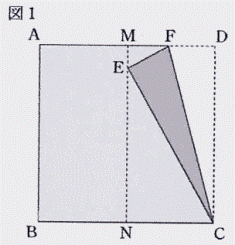 |
| (2) 図2のように,点D が辺AB 上にくるように折り返し,折り目を線分GH とする。 点C,D が移った点をそれぞれI,J とし,線分BH と線分JI との交点をK とする。 AB =9cm,AG =4cmとするとき,四角形GJIH の面積を求めなさい。 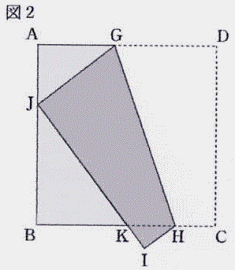 |
| (3) 図3のように,点L をAL:LD =3:2である辺AD 上の点とし,線分LC を折り目として折り返す。 点D が移った点をP,線分LP を延長した直線と辺AB との交点をQ とする。 線分AQ の長さは線分QB の長さの何倍か,求めなさい。 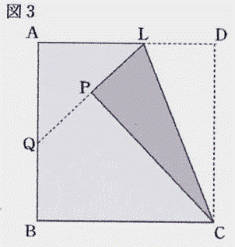 |
| (1) 図1のように,辺AD,BC の中点をそれぞれ点M,N とする。 折り目が点C を通り,点D が線分MN上にくるように折り返す。 点D が移った点をE とし,折り目を線分FC とする。 ∠ EFC の大きさを求めなさい。  |
| 解説 |
EとBを結ぶ。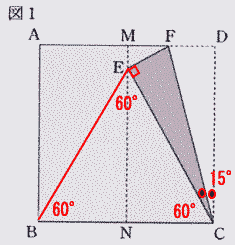 EC = DC(正方形の1辺)なので BC=EC=ED なので 三角形BECは正三角形 ∠ECB = 60° よって ∠DCE = 90 – 60 = 30° ∠FCE = ∠FCD = 30÷2 = 15° ∠FEC = ∠FDC = 90° ∠EFC = 90 – 15 = 75° |
| 答 75° |
| (2) 図2のように,点D が辺AB 上にくるように折り返し,折り目を線分GH とする。 点C,D が移った点をそれぞれI,J とし,線分BH と線分JI との交点をK とする。 AB =9cm,AG =4cmとするとき,四角形GJIH の面積を求めなさい。  |
| 解説 |
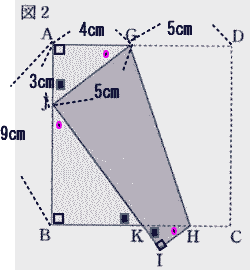 |
| 四角形GJIH =四角形GDCH よって 台形GDCHの上底9-4=5, 高さ9cm なので、下底HC=HIの長さを求めると良い。 図のように △AGJ ∽ △BJK ∽ △IHK AG:GJ:JK=4:5:3 の直角三角形 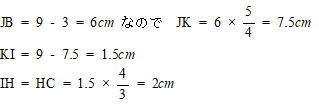 四角形GJIH は台形なので、面積は (5+2)×9÷2=31.5 |
| 答 31.5c㎡ |
| (3) 図3のように,点L をAL:LD =3:2である辺AD 上の点とし,線分LC を折り目として折り返す。 点D が移った点をP,線分LP を延長した直線と辺AB との交点をQ とする。 線分AQ の長さは線分QB の長さの何倍か,求めなさい。  | ||
| 解答 | ||
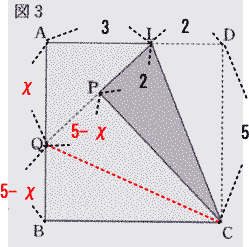 | ||
| AQの長さをχとすると、QB=5-χ 図のように点QとCを直線で結ぶ。 LD=LP=2, PQ=QB=5-χ ⊿AQLにおいて ∠LAQ=90°なので、三平方の定理より | ||
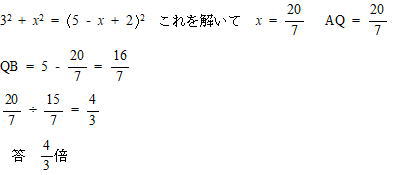 | ||
オンライン家庭教師も在籍中!「お問い合わせ種別」の欄を選択ください。
営業時間:AM 10:00 〜PM 9:00