昭和大学医学部数学過去問対策

プロ家庭教師集団スペースONEは有名進学塾、予備校のカリキュラムに精通し、超難関中学・医学部受験・不登校・学力不振等多様な指導経験15年以上のプロ家庭教師たちが設立したプロ集団です。

スペースONEの医学部受験専門プロ家庭教師が医大・医学部の入試問題を詳しく解説します。

昭和大学医学部過去問研究2020年度(Ⅰ期)数学入試問題

こんにちは　医学部受験専門プロ家庭教師の田中八郎です。 2021年度から数学・国語の選択制になりますが、2020年度は英語数学同一時間で140分配点各100点でした。

数学は例年通り大問4題構成で、[1]，[2]が大問、[3][4]が小問集合でした。
出題内容は[1]座標平面　[2]数列　[3](1)双曲線　(2)確率　(3)確率と期待値　[4](1)微分 (2)関数　(3) 領域の体積でした。

今回は2.数列の漸化式を解説します。 (2)は両辺を同じ形にするために両辺に2n-1をかけます。(3)の3項間漸化式特有の解法です。

昭和大学医学部2020年度Ⅰ期数学入試問題2.数列の漸化式　問題

昭和大学医学部2020年度Ⅰ期数学入試問題2.数列の漸化式　(1)　解説

この問題に対して、昭和大学からは「この問題において正答が存在しないことによる出題不備により、全員正解扱いとする」という説明がありました。

文責田中は「この数列の問題は第n +1項、第n項、第n-1項の関係式(3項間漸化式)の形で出題されていますが、通常このタイプ(3項間漸化式)は初期条件として第1項と第2項が与えられていなければ解けません。

本問では初項(第1項)しか与えられていないので解けません。条件不足ということになる」と思います。

昭和大学医学部2020年度Ⅰ期数学入試問題2.数列の漸化式(2)解説解答

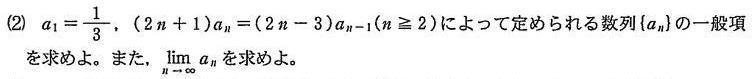
解説解答


昭和大学医学部2020年度Ⅰ期数学入試問題2.数列の漸化式(3)解説解答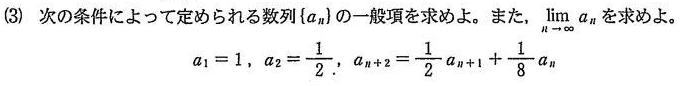


解説解答