女子学院中学校算数過去問研究
2015年度女子学院中学校理科入試問題は 例年通り大問4題構成で、生物・地学・化学・物理分野からの出題でした。
今回は4.浮力を解説します。浮力に関する基礎知識が無くても誘導に従って解く出題でした。
理科入試問題 4. 浮力にチャレンジ
記事の作成者:プロ家庭教師集団スペースONEとは
女子学院中学校2015年度理科入試問題Ⅳ.浮力
2015年度女子学院中学校理科入試問題は 例年通り大問4題構成で、生物・地学・化学・物理分野からの出題でした。
今回は4.浮力を解説します。浮力に関する基礎知識が無くても誘導に従って解く出題でした。
理科入試問題 4. 浮力にチャレンジ

| 1.木片A~Eと水の密度を大きい順に並べたとき、水は何番目になりますか。ただし、水のc㎥あたりの重さは1gです。 |
| 解説 |
| 木片の体積は 10×30×15 = 4500c㎥ |
| 物体の密度 = 物体の重さ(g) ÷ 物体の体積(c㎥) なので |
| 木片A,B,C,D,Eの密度は |
| A: 4050÷4500 = 0.9 |
| B: 3150÷4500 = 0.7 |
| C: 5850÷4500 = 1.3 |
| D: 4950÷4500 = 1.1 |
| E: 3825÷4500 = 0.85 |
| よって 木片の密度の大きさは C(1.3)>D(1.1)>A(0.9)>E(0.85)>B(0.7) 水の密度は1なので、DとAの間 3番目 |
| 答 3番目 |
| 別解 |
| 木片A~Eの体積はすべて4500c㎥なので、木片の重さによって密度の大小関係が決まる。 水のc㎥あたりの重さは1gなので、体積が4500c㎥のとき水の重さは4500g になる。 このことから、大小関係はC(5850g)>D(4950g)>水(4500g)>A(4500g)>E(3825g)>B(3150g) したがって 水は3番目になる。 |
| 答 3番目 |
| 2. この実験結果から考えて、木片が水の浮かぶのはどのようなときか。解答欄の文を完成させなさい。 |
| 解説 |
| 水に浮かんだA,B,Eの密度はA=0.54,B=0.7,E = 0.85。沈んだC,Dの密度はC = 1.3,D = 1.1より水の密度1.1より密度が大きいときに木片は沈み、密度が小さいときに木片が浮かぶことがわかる。 |
| 答 木片の密度が水の密度より小さいとき |
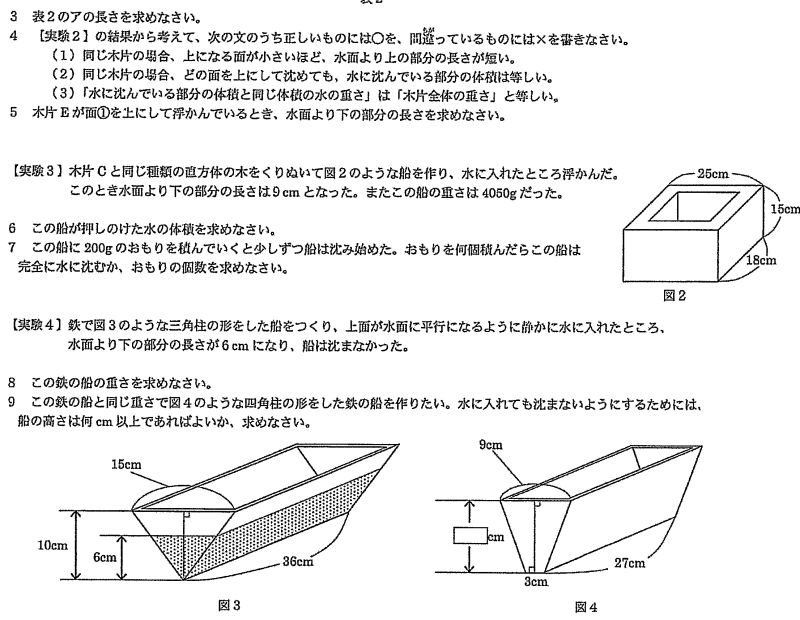
| 3. 表2のアの長さを求めなさい。 |
| 解説 |
 |
| 木片Bの重さは3150g,①の面積は 10×30 = 300c㎡, ②の面積は 10×15 = 150c㎡, ③の面積は 15×30 = 450c㎡ |
 |
| 水面より下の部分の体積は ②の場合 150×210 = 31500c㎥, ③の場合 450×7 = 31500c㎥ |
| ②③の場合と同様 ①の場合も水面より下の部分の体積は、木片の重さと同じ体積31500c㎥なので、 |
| 31500÷300 = 10.5cm |
| 別解1 |
| 木片Bの重さは3150g,体積は4500c㎥なので密度は3150÷4500 = 0.7 |
| 水中にある部分の体積の割合 = 物体の密度÷水の密度 なので 木片の水中にある部分の体積の割合は 0.7÷1 = 0.7 |
| 木片Bは直方体なので ①が上になるときの高さは15cm |
| よって 水面より下の部分の長さは 15×0.7 = 10.5cm |
| 別解2 |
 |
| 答 10.5cm |
| 4. 【実験2】の結果から考えて、次の文の内正しいものには○を、間違っているものには×を書きなさい。 (1) 同じ木片の場合、上になる面が小さいほど、水面より上の部分の長さが短い。 (2) 同じ木片の場合、どの面を上にして沈めても、水に沈んでいる部分の体積は等しい。 (3) 「水に沈んでいる部分の体積の水の重さ」は、「木片全体の重さ」と等しい。 |
| 解説 |
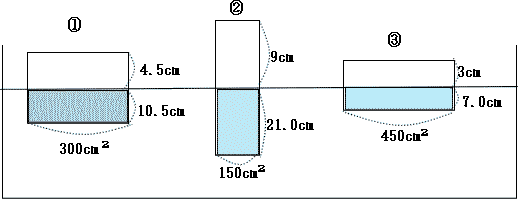 |
| (1) 図の通り 水面より上の部分の長さは①:4.5cm,②9cm,③3cm したがって × |
| (2) 水に沈んでいる部分の体積は全て3150c㎥ よって ○ |
| (3) (2)の結果より○ |
| 4 (1) 木片Aの場合で計算してみると 上になる面が①の場合 (①の面積)=10×30=300c㎡、(水面より上の部分の長さ)=15-13.5=1.5㎝ 上になる面が②の場合 (②の面積)=15×10=150c㎡、(水面より上の部分の長さ)=30-27=3.0㎝ 上になる面が③の場合 (③の面積)=30×15=450c㎡、(水面より上の部分の長さ)=10-9=1.0㎝ 以上の結果から、上になる面が小さいほど、水面より上の部分の長さは短くなるので×。 (2) 木片Aの場合で計算してみると 上になる面が①の場合 (水に沈んでいる部分の体積)=13.5×10×30=4050c㎥ 上になる面が②の場合 (水に沈んでいる部分の体積)=27×15×10=4050c㎥ 上になる面が③の場合 (水に沈んでいる部分の体積)=9.0×15×30=4050c㎥ 以上の結果から○。 (3) (2)の計算結果を見ると、水に沈んでいる部分の体積はすべて4050c㎥で、木片の重さと値が同じなので○。 実験2の結果から「浮力の大きさは物体が押しのけた水の重さに等しい。」 |
| 答 (1) × (2)〇 (3)〇 |
| 5.木片Eが面①を上にして浮かんでいるとき、水面より下の部分の長さを求めなさい。 |
| 解説 |
| 木片Eの重さは3825gなので、水に沈む部分の体積は3825c㎥ |
| ①の面積は10×30 = 300c㎡ |
| 水面より下の部分の長さは 3825÷300 = 12.75cm |
| 別解1 |
| 木片Eの重さは3825g,体積は4500c㎥なので、木片Eの密度は 3825÷4500 = 0.86 |
| 木片の水中にある部分の体積の割合は 0.85÷1 = 0.85 水に沈む部分の体積は3825c㎥ |
| ①を上にして浮かんでいるとき高さは15cmなので 下の部分の長さは15×0.85=12.75cm |
| 別解2 |
| 4(3)「水に沈んでいる部分の体積の水の重さ」は、「木片全体の重さ」と等しいので |
| 3825÷10÷30 = 12.75 |
| 答 12.75cm |
| [実験3] 木片Cと同じ種類の直方体の木を切り抜いて 図2のような船を作り、水を入れたところ浮かんだ。このとき水面より下の部分の長さは9cmとなった。またこの船の重さは4050gだった。 |
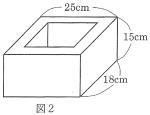 |
| 6. この船が押しのけた水の体積を求めなさい。 |
| 解説 |
| 「水に沈んでいる部分の体積の水の重さ」は、「船全体の重さ」と等しいので、船の重さ4050gがこの船が押しのけた水の体積4050c㎥ |
| 答 4050c㎥ |
| |
| 別解 |
| 6 船の底の面積は、18×25c㎡なので、押しのけた水の体積は18×25×9=4050c㎥。 |
| 答 4050c㎥ |
| 7. この船に200gのおもりを積んでいくと少しずつ船は沈み始めた、おもりを何個積んだらこの船は完全に水に沈むか、おもりの個数を求めなさい。 |
| 解説 |
| 水面より上に出ている船の体積は 25×18×(15 – 9) = 2700c㎥ よって 2700g以上のおもりを積めばよいので 2700÷200 = 13.5 したがって おもりの数は14個 |
| 別解1 |
 |
水面下の体積が4050c㎥なので 6750 – 4050 = 2700c㎥ 分の重さが加われば沈む。 よって 2700g÷200 = 13.5 14個のおもりを積めばよい。 |
| 別解2 |
| 船が完全に沈むとき船の高さ15cmが水面下にある。 浮力の大きさは物体が押しのけた水の重さに等しいから、「水面下の体積=船の重さ+おもりの重さ」となる。 よって (15×28×18 – 4050)÷200 = 13.5 |
| 答 14個 |
| [実験4]鉄で図3のような三角柱の形をした船をつくり、上麺が水面に平行になるように静かに水を入れたところ、水面より下の部分の長さが6cmになり船は沈まなかった。 |
| 8. この鉄の船の重さを求めなさい。 |
| 解説 |
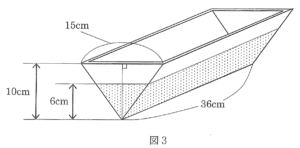 |
| 船の底面積と水面下の部分の相似比は 10:6 = 5:3より 船の底面積と水面下の部分の底面積の比は5×5:3×3 高さ36cmが等しいので船の体積と水面下の部分の体積はも 5×5:3×3 よって 水面下の部分の船の体積は したがって、この鉄の船の重さは 972g |
| 別解 |
| 船の体積と水面下の部分の体積の比は5×5:3×3 = 25:9 なので |
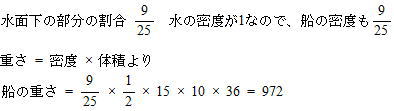 |
| 答 972g |
| 9. この鉄の船と同じ重さで図4のような四角柱の形をした鉄の船を作りたい。水に入れても沈まないようにするためには、船の高さは何cm以上であればよいか。求めなさい。 |
| 解説 |
 |
| 船の重さが972gなので、水面下の体積が972c㎥になるときの高さは (9 + 3)×□÷2×27 = 972 □ = 972÷27×6) □ = 6 したがって 6cmの深さまで船は沈むので、沈まないようにするためには6cm以上であればよい。 |
| 別解 |
| 水面下の部分の割合が1以上であれば船は沈まないので 密度も1 体積 = 船の重さ÷1 なので 体積 = 972c㎥ よって (3 + 9) ×□÷2 = 972 よって □ = 6 |
| 答 6cm |
オンライン家庭教師も在籍中!「お問い合わせ種別」の欄を選択ください。
営業時間:AM 10:00 〜PM 9:00