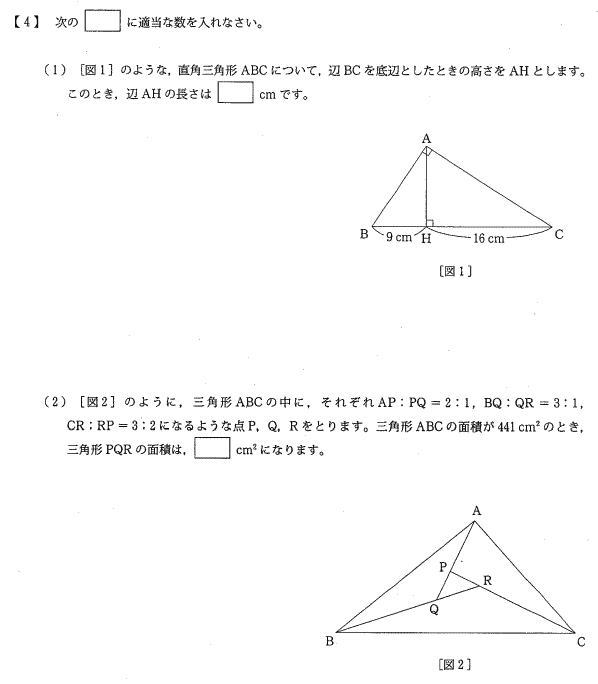
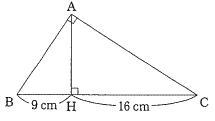
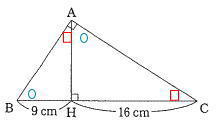
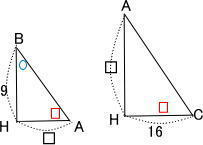
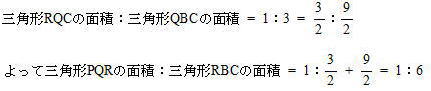慶応義塾中等部2010年度算数入試問題4.相似比と面積比 |プロ家庭教師集団スペースONE【公式】

慶應義塾中等部算数過去問研究

2010年度慶応義塾中等部算数入試問題は　１．２．３が計算２問を含む小問集合計１０問　４．平面図形　５．平面図形　６．仕事算　７．水槽とグラフ　８．平面上の点移動　が出題されました。一行問題は特殊算全分野から満遍なく出題されていますが、大問は非常に出題分野に偏りがあり、平面図形の占める割合が非常の大きいものでした。解答は途中式を必要としない解答欄に数字のみを書き込む形式でした。

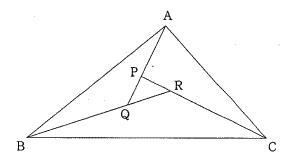
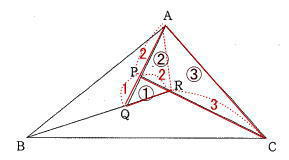
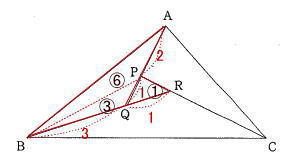
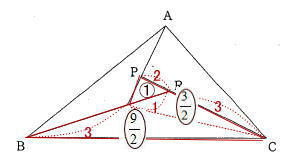
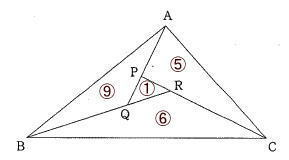
今回は　慶応義塾中等部算数入試問題頻出の図形問題から４番を解説します。

算数入試問題　平面図形にチャレンジ

慶応義塾中等部2010年度　算数入試問題　4.相似比と面積比問題

慶応義塾中等部2010年度　算数入試問題　4.相似比と面積比(1)解説解答

(1)　［図１］のような、直角三角形について、辺ＢＣを底辺としたときの高さをＡＨとします。このとき、辺ＡＨの長さは□ｃｍです。
解説
図のように三角形ＡＢＨと三角形ＣＡＨは相似形

それぞれに対応する辺はＡＢ：ＨＡ，ＢＡ：ＡＣ，ＡＨ：ＣＨ
ＡＨの長さを□とおいて、比例式であらわすと

９：□＝□：１６ □×□＝９×１６ □×□＝３×３×４×４ □＝３×４
答　　　１２

慶応義塾中等部2010年度　算数入試問題　4.相似比と面積比(2)解説解答

(2)　［図２］のように、三角形ＡＢＣの中に、それぞれＡＰ：ＰＱ＝２：１，ＢＱ：ＱＲ＝３：１，ＣＲ：ＲＰ＝３：２になるような点Ｐ，Ｑ，Ｒをとります。三角形ＡＢＣの面積が４４１ｃ㎡のとき、三角形ＰＱＲの面積は□ｃ㎡になります。

解説
高さの等しい三角形は辺の比＝面積比であることを利用して解きましょう。
三角形PQRの面積を１にします。
まず三角形PQRと三角形APCから考えましょう。

PQ：AP＝１：２　　なので三角形PQRの面積：三角形APRの面積 = 1：2 三角形APRと三角形ARCは PR：RC＝２：３　　なので三角形APRの面積：三角形ARCの面積＝２：３よって　　　三角形PQRの面積：三角形APCの面積＝１：２＋３＝１：５
三角形PQRと三角形APCにおいて

三角形PQRと三角形PBQは　QR：BQ＝１：３　なので　三角形PQRの面積：三角形PBQの面積＝１：３三角形PBQと三角形ABPは　QP：PA＝１：２　なので　三角形PBQの面積：三角形ABPの面積＝３：６よって　三角形PQRの面積：三角形APCの面積＝１：３＋６＝１：９
三角形PQRと三角形RBCにおいて

⊿PQRと⊿RQCは　PR：RC＝２：３　なので三角形RQCと三角形QBCはRQ：QB＝１：３　なので
以上のことから三角形PQRの面積：三角形ABCの面積＝(１)：(１)＋(５)＋(９)＋(６)＝(１)：(21) (21) = 441ｃ㎡なので (１) ＝４４１÷２１＝２１ｃ㎡
答　　　２