聖光学院中学校帰国生算数過去問対策

2019年度聖光学院中学帰国生算数入試問題は例年通り大問5題構成で、出題内容は１．四則計算1問,場合の数1問，立体図形の切断, 2.流水算，3.平面図形，4.場合の数，5.整数の性質でした。

今回は1.(2) 確率を解説します。樹形図をうまく使いましょう。

聖光学院中学校帰国生入試問題解説解答を頒布中です。メールpro.tutor@ws-spaceone.jpでお問い合わせください。

聖光学院中学校　2019年度帰国生算数入試問題　場合の数　問題

(2)　100から999までの3桁の整数900個の中で、百の位，十の位，一の位のうちちょうど2つだけが同じであるものは全部で何個ありますか。

聖光学院中学校　2019年度算数入試問題　場合の数　解説解答

(2) ①　3桁のそれぞれの位の数が3つともに同じであるもの
　　　　　　　 111，222，333，・・・・・・・，999 　　　　9通り

②　3桁のそれぞれの位が3つとも異なるもの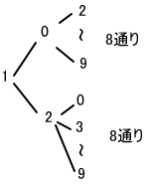


百の位が1のとき　十の位は0,2，3，4，5，6，7，8，9 　の9通り
　　その1通りずつに対して一の位は8通りあるから
　　9×8 = 72通り・・・(ⅰ)

百の位が2，3，・・・・，9のときもそれぞれ72通りある　ので、

9×72= 648通り・・・(ⅱ)

①，②(ⅰ)，(ⅱ)より　900 – (9 + 648) = 243個・・・答え

別解１

(2) ①　3桁のそれぞれの位の数が3つともに同じであるもの
　　　　　　　 111，222，333，・・・・・・・，999 　　　　9通り

②　3桁のそれぞれの位が3つとも異なるもの
　　積の公式より　9×9×8 = 648 　　　648通り

①，②　より　900 – ( 9 + 648) = 243個・・・答

別解2.

2個使う数字が0のとき

100,200,……,900の9通り•••(ⅰ)

・2個使う数字が1〜9のとき

たとえば1を2個使うとき

残りの1つの数字が0のとき

101と110の2通り•••(ⅱ)

残りの1つの数字が2〜9のとき

たとえば2のとき

112と121と211の3通り

2だけでなく2〜9の8通りあるので

3×8=24通り•••(ⅲ)

以上(ⅱ)と(ⅲ)より2つ使う数字が1のときに3+24=27通り

1だけでなく1〜9の9通りあるから、27×9=243通り•••(ⅳ)

(ⅰ)，(ⅳ)より　　9 + 234 = 243通り　　　•••(答え)

プロ家庭教師集団スペースONEプロ家庭教師の聖光学院中学帰国入試過去問解説解答を頒布中です。メールでお問い合わせください。