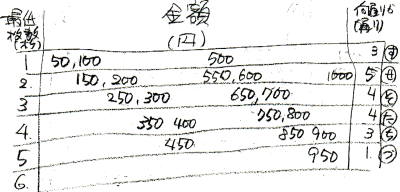2020年度　開成学園　開成中学校算数入試問題

開成学園　開成中学校過去問対策

2020年度の開成中学校算数入試問題は、[1]が例年の四則計算も小問集合も無くなり、大問4題構成でした。
１．条件付き速さの問題。2.円周上の点移動。3.場合の数。4.空間図形。が出題されました。

全問共に難易度が高く煩雑な条件を的確に読み取る能力が要求される問題ぞろいでした。

開成中学算数の配点は85点。2020年度算数合格者平均得点49.5点，受験者平均得点38.6点，合格者平均得点率58%でした。

今回は　3.場合の数を解説します。お金の支払方法を、条件をくみ取って当てはまらない場合を除く的確さを求められます。

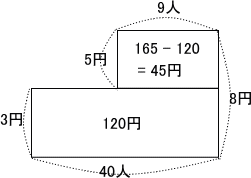
(1)(イ)は(ア)を正答すれば鶴亀算で簡単に求められます。

(2)は全ての場合を書き出していると時間内に終わらなくなるので、ではどうやって簡略して解いていけばよいかを説明します。

開成中学受験指導はスペースONEのプロ家庭教師にお任せください。

開成中学校2020年度　算数入試問題　3.場合の数　問題