2020年度帰国生入試問題は非公開です。今回は2019年度入試問題 1.四則計算 2.小問集合 3.場合の数 4.旅人算 5.平面図形 から、5.平面図形を解説します。正方形の性質と相似形を用いて解きましょう。
聖学院中学校2019年度帰国生 算数入試問題 5.平面図形 問題
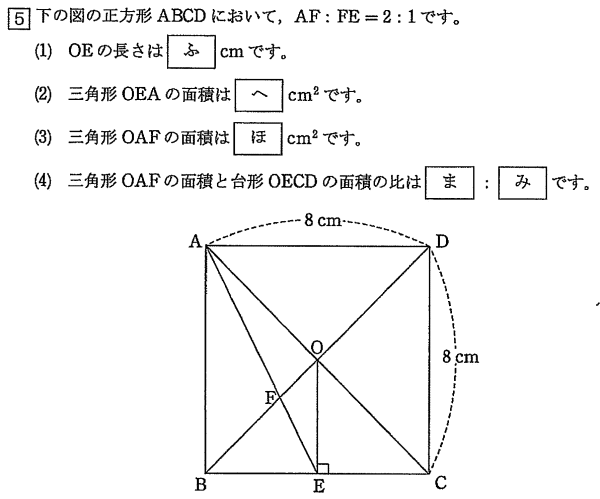
聖学院中学校2019年度帰国生 算数入試問題 5.平面図形 (1) 解説解答
解説解答
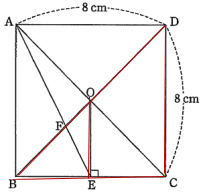
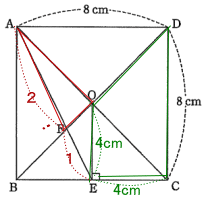
点Oは正方形の対角線の交点で、交点から辺BCに垂線を下ろした足が点E。よって BE = EC 三角形BEOと三角形BCDは相似形なので、BE:BC = OE:OC = 1:2
CD = 8cm なので、OE = 4cm
答 4cm
聖学院中学校2019年度帰国生 算数入試問題 5.平面図形 (2) 解説解答
(2) 三角形OEAの面積は[へ]c㎡です。
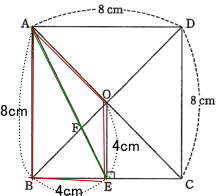
三角形OEAの面積 = 台形OEBAの面積 – 三角形AEBの面積
台形OEBAの面積:上底OE = 4cm,下底AB = 8cm,高さEB = 4cm
三角形AEBの面積 :底辺AB = 8cm,高さBE = 4cm なので
(4 + 8) ×4 ÷ 2 – 8×4÷ 2 = 8
答 8c㎡
聖学院中学校2019年度帰国生 算数入試問題 5.平面図形 (3) 解説解答
解説解答
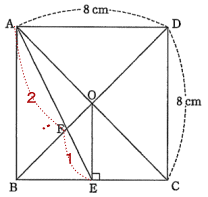
三角形OEAの面積は (2)より8c㎡
AF:FE = 2:1なので 三角形OAFの面積:三角形OFEの面積 = 2:1
よって 三角形OAFの面積は
聖学院中学校2019年度帰国生 算数入試問題 (4).平面図形
解説解答
台形OECDの面積は (4 + 8)×4÷2 = 24c㎡
(4) より三角形OAFの面積は
