攻玉社中学校入試合格のための過去問対策
2020年度攻玉社中学校第1回入試は募集人数100名に対し 応募者453名 受験者430名 合格者179名 合格者最低点204点でした。
算数入試問題は、1.四則計算3問 2.小問集合7問 3.食塩水の濃度の問題 4.立体図形と立体上の点移動が出題されました。
今回は 2.小問集合を解説します。
攻玉社中学校2020年度算数入試問題2.小問集合 問題

攻玉社中学校2020年度算数入試問題2.小問集合 解説解答
長さ500mの橋を通過するのに31秒かかるときに 列車が走る距離は 列車の長さ + 橋の長さ
よって 31秒と16秒の差 31 – 16 = 15秒は 500 – 200 = 300mを列車が走ったときの差になるので、
列車の速さは 300 ÷ 15 = 20m/秒
よって 16秒間で列車が走る距離は 20 × 16 = 320m
トンネルの長さが 200m なので、列車の長さは 320 – 200 = 120m
答 120m
(2) 幅12m,長さ25m,深さ1mの直方体のプールをいっぱいにする水の量は、500mlのペットボトル□本分です。
解説解答
1㎥ = 1000ℓ = 1000000mℓ
プールをいっぱいにする水の量は (12×25×1)㎥ = (12×25×1×1000)ℓ = (12×25×1000000)mℓ
よって 500mℓのペットボトルでは
12×25×1000000÷500 = 600000
答 600000本
(3) ある品物を定価の2o%引きで売ると432円の利益があり、定価の35%引きで売ると216円の損をします。この品物の仕入れ値は□円です。(消費税は考えないものとします。)
解説解答
定価の 35% – 20% = 15% が 432 + 216 = 648円に相当するので、
定価は 648 ÷0.15 = 4320円
仕入れ値は 定価の20%引きより 432円少ないので
4320 ×(1-0.2) – 432 = 3024
答 3024円
(4) 2020年7月3日は金曜日です。この年の10月28日は□曜日です。
解説解答
1週間は 7日なので、 3日から7日ごとに同じ曜日になる。
7月3日から7月31日までは 31 – 3 = 28日
8月は31日,9月は30日,10月28日までは
28 + 31 + 30 + 28 =117日なので
117 ÷7 = 16 余り5日 金曜日があまり0になるので土曜日から5日後 土日月火水 より 水曜日
答 水曜日
(5) Aさんは、1個160円のリンゴと、1個100円のオレンジを合わせて25個買い、3000円を払いました。
解説解答
オレンジは1個100円なので、お釣りは100円単位で10円玉のお釣りはない。よって リンゴの個数は5の倍数個となる。
リンゴ5個のとき 160×5 = 800円
オレンジは 25 – 5 = 20個,2000円,
よって 合計2800円 お釣りは200円となり オレンジの追加は2個でおつりなし。
リンゴ10個のとき 160×10 = 1600円
オレンジは 25 – 10 = 15個 1500円で合計金額は 3100円となり、不足になる。
したがって 買ったオレンジは全部で 20 + 2 = 22個
答 22個
(6) ある製品を作るたの機械があります。その製品は、Aを1台,Bを1台使って作ると30時間かかります。同じ製品を、Bを1台,Cを1台使って作ると36時間かかり、Aを1台,Cを1台使って作ると45時間かかります。このとき、同じ製品をAを1題使って作ると□時間かかります。
解説解答
製品を作る仕事量を 30 と 36 と 45の最小公倍数の180 とすると、
Aを1台,Bを1台の1時間の仕事量は 180 ÷ 30 = 6
Bを1台,Cを1台の1時間の仕事量は 180 ÷36 = 5
Aを1台,Cを1台の1時間の仕事量は 180 ÷45 = 4
A1台 + B1台 + B1台 + C1台 + A1台 + C1台それぞれの1時間の仕事量の合計は
2 × (A + B + C) = 6 + 5 + 4
A + B + c = 14÷2 = 7.5
B1台とC1台の1時間の仕事量は 5なので、A1台の1時間の仕事量は 7.5 – 5 = 2.5
よって A1台で作るときにかかる時間は 180 ÷ 2.5 = 72
答 72時間
(7) AB = 10cm,BC = 8cm,角Cが直角の直角三角形ABCがあります。下の図のように、点Bを中心として、反時計回りに90°だけ回転させたとき、辺ACが通った部分(図の斜線部分)の面積は□c㎡です。
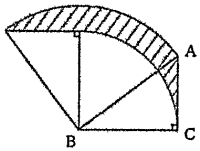
解説解答
斜線部分の面積 = (三角形ABCの面積 + 半径AB = 10cm中心角90°の扇形の面積) – (三角形ABCの面積 + 半径BC = 8cm中心角90°の扇形の面積) なので
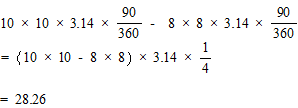
答 28.26c㎡
