2021年度早稲田実業学校中等部入学試験は2月1日に実施され、合格発表は2月3日 13:00 ~(専用ウェブサイト)で行われました。
入試科目は
国語(100点満点/60分),算数 (100点満点/60分),社会 (50点満点/30分),理科 (50点満点/30分)で面接はありません。
募集人員は、一般入試(男子85名,女子40名),帰国生男女合計3名以内に対し、一般入試応募者数男子361名女子215名,受験者数男子329名,女子195名 合格者男子102名,女子50名 帰国生出願数 男子6名,女子2名,受験者数男子5名,女子2名,ごうっかう者3名,女子0名でした。
早稲田実業学校中等部入試問題傾向と対策
2021年度 算数入試問題は、1.小問集合4問 2.小問2問 流水算,場合の数 3.割合の文章題 4.場合の数 5.平面図形と規則性が出題されました。
今回は 2.(1)流水算の出会いと追いかけを解説します。船が出会いおいける場合の距離は通過算と同様です。
早稲田実業学校中等部2021年度算数入試問題 2.(1)流水算 問題

早稲田実業学校中等部2021年度算数入試問題 2.(1)流水算 ① 解説解答
(1) 船Aの静水での速さは秒速何mですか。
解説解答
船Bが船Aに追いついてから完全に追い越すまでに 船Bが進んだ距離は船Aと船Bの長さの和なので 56 + 28 = 84m
船Bが船Aを追い越したので この時の速さの差は 船Bの静水時の速さ – 川の流れの速さ – (船Aの川の流れの速さ – 川の流れの速さ) = 船Bの静水時の速さ – 船Aの静水時の速さ
船Bが船Aに追いついてから完全に追い越すまでにかかった時間は 1分10秒 = 70秒
よって 船Bの静水時の速さ – 船Aの静水時の速さ = 84÷ 70 = 1.2m/秒
また 船Aと船Bが出会ってから完全に離れるまでにかかった時間は 10.5秒 船Aは上り、船Bは下りっているので 速さの和 = 船Aの静水時の速さ – 川の流れの速さ + (船Bの川の流れの速さ + 川の流れの速さ) = 船Aの静水時の速さ + 船Bの静水時の速さ
よって 線分図の通り
船Aの静水での速さは (8 – 1,2) ÷ 2 = 3.4
答 秒速3.4m
早稲田実業学校中等部2021年度算数入試問題 2.(1)流水算 ② 解説解答

解説解答
いつもの川の流れと2倍になったときの川の流れの比は ①:②
かかった時間の比は![]()
よって 速さの比は [14]:[11]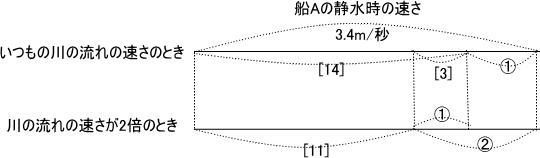
線分図の通り ① = [14]なので
3.4m/秒 = [14] + [3] = [17]
したがって いつもの川の流れの速さは![]()
答 0.6m/秒
