相似形を用いた解法
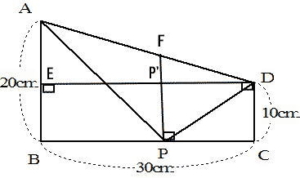
点Dから辺ABに垂線を引き辺ABとの交点をEとする。また辺AD上の点Fが角FPC=角Rとなるようにおき、辺FPと辺DEとの交点をP’とする。
三角形APDは辺EDと辺FPが直角に交わったタコ形の四角形で面積を求められる。辺ED=30cm, 面積は210c㎡ 辺FP=210×2÷30=14 P’P=10cm よって 辺FP’=4cm
記事の作成者:プロ家庭教師集団スペースONEとは
中学受験の特殊算平面図形の求積の解法(低学年からの中学受験)
中学受験の特殊算の解法は1つではありません。様々な解法にチャレンジしましょう!
今回は平面図形の問題を通して特殊算の解法を解説します。
類題は2007年度城北中学校でも出題されています。
算数入試問題 平面図形にチャレンジ
問題
次の図のような台形ABCDがあります。点Pは辺BC上の点で、三角形APDの面積が210c㎡のとき、PCの長さは何cmですか。(慶応中等部)
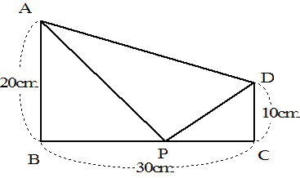
下の図のように補助線を引いて、長方形を二つ描いてみよう。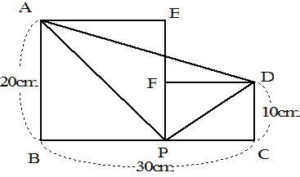
三角形ABP+三角形DCPの面積は240c㎡
下図のように二つの長方形の面積は480c㎡ となる。これはつるかめ算の面積図解法と同じになります。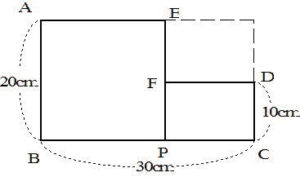
まず2つの三角形△ABP+△DPCを求めます。
台形ABCD = (20+10)×30÷2 = 450 よって 450 - 210 = 240(c㎡)
もしCDの長さがABと同じ20㎝だったら、20㎝のときの点をD’とすると △ABP + △D’PC = ABCD’÷2となるので
ABCD’÷2 = 20 × 30 ÷ 2 = 300(c㎡)
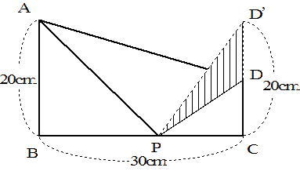
これより図の三角形△PD’D = 300 - 240 = 60(c㎡)となります。PCの長さは△PD’Dの高さと等しいので
DD’= 10㎝ より CP = 60 × 2 ÷ 10 = 12
よって12㎝ 答え 12 cm
解法2で使った図形の面積の性質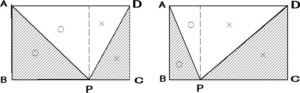
Pがどこにあってもまた下のような図形でも斜線の部分の面積は長方形ABCDの2分の1
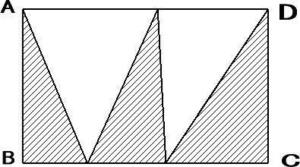
ADと平行にPから直線を引いてDCを延長した直線との交点をEとすると
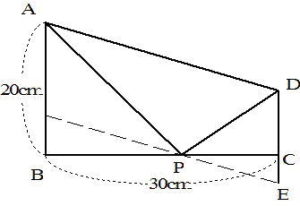
ADを底辺とするとPを頂点としたときもEを頂点としたときも高さが等しくなるので
(△APDの面積)=(△AEDの面積)となります。
よって、△AEDの面積は 210 c㎡ となるので
△AEDの底辺をDEとしたとき、高さは30cm より DE=210×2÷30 から DEは 14cm となります。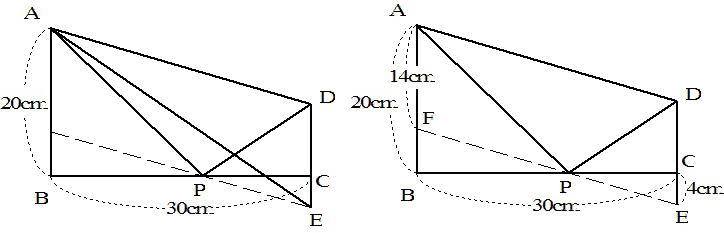
上図のようにPEの延長とABとの交点Fをとると AF=14cm より FB=6cm
△FBPと△ECPは相似なので、相似比は AF:EC=3:2よりPB:PC=3:2だからPC=30÷5×2=12
答え12cm
解法3で使った図形の性質は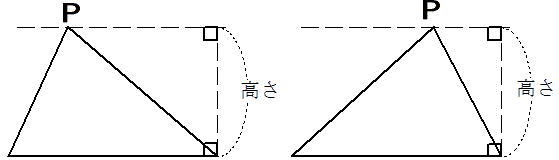
ABと平行にPを移動すればPがどこにあっても△ABPの面積は底辺はAB、高さは同じなので、いつも同じというどちらも三角形の面積の性質を使っています。
問題によっていろいろな性質を使い分けられるようにししましょう。
平面図形の求積 解法4
三角形APDは辺EDと辺FPが直角に交わったタコ形の四角形で面積を求められる。辺ED=30cm, 面積は210c㎡ 辺FP=210×2÷30=14 P’P=10cm よって 辺FP’=4cm
三角形APDは辺EDと辺FPが直角に交わったタコ形の四角形で面積を求められる。辺ED=30cm, 面積は210c㎡ 辺FP=210×2÷30=14 P’P=10cm よって 辺FP’=4cm
三角形AEDと三角形FP’Dは相似で、相似比は⑤:②
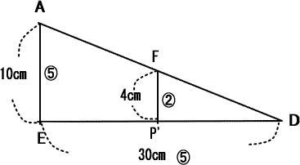
よって辺P’D=PCの長さは 30÷5×2=12cm
以上の解法以外に中学生以上でしたら、当然辺PCの長さをXとおく連立方程式でも解けますが、小学生の算数としては論外としかいえないでしょう。
オンライン家庭教師も在籍中!「お問い合わせ種別」の欄を選択ください。
営業時間:AM 10:00 〜PM 9:00