ラ・サール高等学校数学過去問研究
2016年度ラ・サール高等学校数学入試問題は例年通りの出題構成で1.計算問題 2.小問集合 3.~6.大問でした。出題内容は 1.計算問題4問 2.小問集合5問 3.関数のグラフ 4.平面図形 5.確率 6.立体図形でした。
今回は 4. 平面図形を解説します。内角に注意し補助線を引いて考えましょう。
ラ・サール高校2016年度 数学入試問題 4.平面図形 問題
図のような四角形ABCDについて、次の問いに答えよ。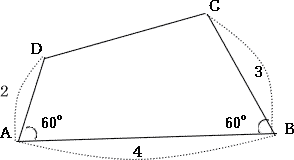
(1) CDの長さを求めよ。
(2) 3点A,D,Cを通る円をOとする。円Oの半径を求めよ。
(3) (2)の円Oと、直線ABの交点のうち、Aでない方をEとする。BEの長さを求めよ。
解説解答
| (1) 解説解答 |
| (1) CDの長さを求めよ。 |
| 解説解答 |
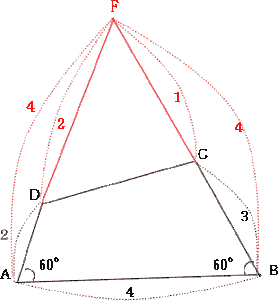 |
| ADの延長線とBCの延長線の交点をFとする。∠FAB = ∠FAB = 60°より∠AF = 60° よって △ABFは正三角形 △DFCにおいて、 DF = 4 – 2 = 2, FC = 4 – 3 = 1,∠AFB = 60°なので △DFCの各辺の比は |
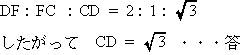 |
頒布中入試問題解説解答
| (2) 解説解答 |
| (2) 3点A,D,Cを通る円をOとする。円Oの半径を求めよ。 |
| 解説解答 |
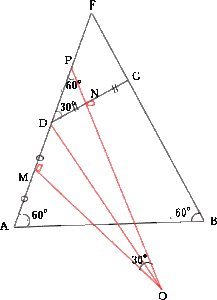 |
| 外心は三角形の3辺の垂直二等分線の交点なので、 図の通り外心をO,ADの中点をM,DCの中点をN,ONの延長線とDEとの交点をPとおく。 ∠DNO = 90°なので ∠DNP = 90° (1)より∠EDC = 30°よって ∠DPN = 60°・・・① 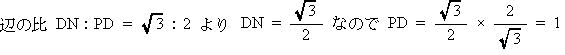 ∠PMO = 90°・・・② △MOPにおいて、 ①,②より∠MOP = 30° PM = MD + DM = 2 △DMOにおいて、三平方の定理より 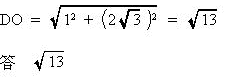 |
頒布中入試問題解説解答
| (3) 解説解答 |
| (3) (2)の円Oと、直線ABの交点のうち、Aでない方をEとする。BEの長さを求めよ。 |
| 解説解答 |
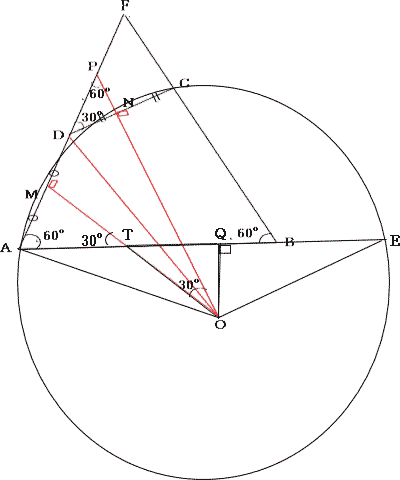 |
| 点OからAEに垂線をおろし、その交点をQ,AEとMOとの交点をTとする。 △ATMと△OTQにおいて、∠ATM = ∠OTQ = 30°(対頂角) ∠TMA = ∠TQO = 90° したがって △ATM ∽ △OTQ |
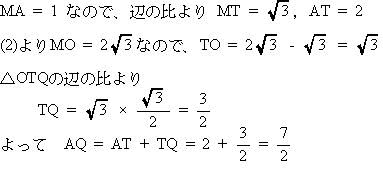 |
| △AOQと△EOQにおいて、∠OQA = ∠OQE = 90° OQ = OQ (共通) OA = OE (半径) したがって △AOQ ≡ △EOQ |
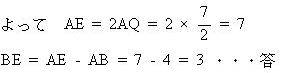 |
